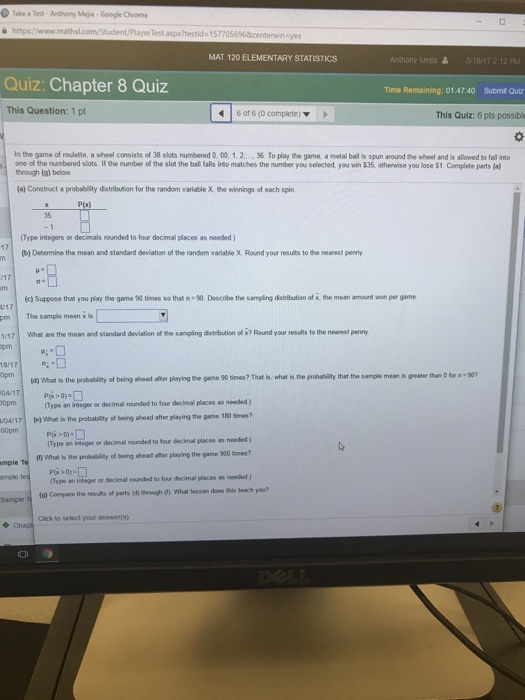
Roulette Probability Questions

Roulette Probability Questions Rating: 5,8/10 3919 reviews

In the game Roulette, a ball spins on a circular wheel that is divided into 38 arcs of equal lenght, numbered 00, 0, 1, 2, ... , 35, 36. The number on the arc on which the ball stops is the outcome of one play of the game. The numbers are also colored as follows:
1, 3, 5, 7, 9, 12, 14, 16, 18, 19, 21, 23, 25, 27, 30, 32, 34, 36 are red,
2, 4, 6, 8, 10, 11, 13, 15, 17, 20, 22, 24, 26, 28, 29, 31, 33, 35 are black,
0, 00 are green
Define the following events:
These are the values i got not sure if they are right
A: Outcome is an even number (0 and 00 are considered neither odd nor even) = 9/19
B: Outcome is a red number = 9/19
C: Outcome is a green number = 1/19
D: Outcome is a low number (1-18) = 9/19
(a) P(C) = 1/19
(b) P(AnB) = 4/19
(c) P(BuCuD) =
a and b are right i dont know how to get c
Thank you!

Assuming you have an American roulette wheel (with 38 slots, not 37), the probability of that event is 1/38^6. No one is astonished by that event, and yet it is exactly the same probability as getting a 15 all six times. Why the discrepancy in what surprises us? The probability of this bet winning is 8.11% in European, and 7.89% in American roulette. The payout for winning a street bet is 11:1. Corner means betting on four numbers that form a square on the table, like 1, 2, 4, and 5, for example. If you spin then pull the trigger, the probability that the shot comes from slot 1 is, indeed, 1/6. However, once the trigger has been pulled (and you are still alive), you have an additional piece of information: The slot was not 2 or 3. Solution for A bet on “black” in Roulette has a probability of 18/38 of winning. If you win, you double your money. You can bet anywhere from $1 to $100 on.

make into disjoint sets and add up
(c) P(BuCuD) = P(B) + P(C) + P(LOW BLACK)
= (18+2+9)/38 = 29/38 <---------

Introduction

Select an event (set of outcomes) of interest and a number of spins on the wheel. The outcome of each spin will be displayed as a bar graph of individual results and as a proportion of times the event of interest occurred. Check the box to show the true probability of the event. Click RESET at any time to start over.

Click the 'Quiz Me' button to complete the activity.

The American roulette wheel has 38 numbered slots: 1 through 36, 0, and 00. If the wheel is fair, the ball will be equally likely to end up in any slot.

In this applet, you can study the behavior of the wheel through a small number of spins, as well as a large number. You can also investigate the probability of certain sets of outcomes (events); does the empirical evidence from the wheel agree with the theoretical model that says:

P(A) = (Number of Outcomes in A) / (Number of Possible Outcomes)

Question 1.1

The applet initially has “Spin a 2” as the event of choice. What is the probability of a 2 on the roulette wheel? Give your answer to 4 decimal places.
kL1fsVqsJt1cTnqcnYwTsg

Roulette Wheel Probability Questions

Incorrect. Only one slot on the wheel has the number 2 out of 38 slots.

Question 1.2

Spin the when 5 times. Do you expect to see a 2? 7zVRuryDpphPQjDfxtKbZg

Incorrect. Something that should happen rarely (less than 5% of the time) would not be expected to occur in five attempts.

Correct. Something that should happen rarely (less than 5% of the time) would not be expected to occur in five attempts.

Question 1.3

Reset the applet and change the sample size to 2000 spins. Do you expect to see a 2? esgbknumN3x7TOMm7lo9Vw

Incorrect. Something that should happen rarely (less than 5% of the time) will be expected to occur in many attempts.

Correct. Something that should happen rarely (less than 5% of the time) will be expected to occur in many attempts.

Question 1.4

Change to spin a red number and five attempts. What is the probability the wheel lands on a red number? Give your answer to four decimal places.
Rnm9i8NtXpOC8Xy3sXm6eg

Incorrect. Eighteen slots on the wheel out of 38 slots are red.

Correct. The probability of a red is 18/38 = 0.4737.

Question 1.5

Did you get a red? esgbknumN3x7TOMm7lo9Vw

Incorrect. If the line in the middle of the output moved anywhere off 0, you got a red.

Correct. It would be highly unusual to not get a red in five spins.

Question 1.6

Reset the applet and spin the wheel 2000 times. This is almost a “very large” number of attempts. What do you see in the center part of the window?
RjPD0yIPeSIdJmSOTGeuarLH0Jta+t6eW/rhKtowtunBaXxIg3PMiZRUuXYYTVeqJuU3JHNPgC/fGUXZxCgLngqqcoBQjN37Yal0iqS6dErNKt/2qnQYRScs55l5ywN1V2t//TUJ52oYABwBcVUkopVZwdf5lAtPdqPCrBQj+CY4TAAJ2q1hy/bsjwzZzUfHftrFaaleoBD2U61ZzaWzSpXVPx+wgzAavn0IVHUgayY=

Roulette Wheel Probability Calculator

Incorrect. Probabilities are about what can happen in the long term. For any event of interest, as the number of trials becomes large, the relative frequency of the event (in this case, the proportion of reds) becomes close to the true probability of the event.

Roulette Probability Example

Correct. Probabilities are about what can happen in the long term. For any event of interest, as the number of trials becomes large, the relative frequency of the event (in this case, the proportion of reds) becomes close to the true probability of the event.